作者:亓玉台 许庆
中冶建筑研究总院有限公司
摘 要
传感器布置方案设计是结构健康监测中最为基础性和关键性的环节,好的传感器布置方案,既要满足结构健康监测的要求,尽可能地减小噪声等误差因素的影响来得到结构的真实响应,又要满足现场环境的要求,还需要尽可能地降低成本。
振动模态分析是目前结构健康监测中应用较多的一种方法,相比于传统的静态检测方法,利用结构的动力响应对结构进行分析可以更好地反映大型结构整体的健康状况,有着更为广阔的应用前景。
由于大型空间结构的形式复杂,自由度较多,在结构振动模态分析的过程中,传感器的布置是其中基础性和关键性的环节。如果传感器布置过少,有可能无法得到结构的真实响应,而布置过多则可能导致数据的冗余,影响实测振型的正交性,且增加了经济成本,给后续的数据处理工作带来负担。此外,工程现场情况的复杂性也对传感器的布置有较大限制。在满足经济性、功能性、现场环境等要求的前提下,如何优化传感器的布置方案,以获得结构最真实的信息,就成为结构健康监测过程中最先要解决的问题。
针对以上问题,本文以模态置信矩阵为评价标准,提出了一种传感器布置的优化方法,并通过模拟试算,给出了具体的优化步骤及实施建议。
1
模态置信矩阵法原理
结构的振动可以视为各阶振型的叠加。对于有限自由度结构体系,结构动力响应为:
{ u }=[ Φ ]{ q }
(1)
式中:{ u }为结构动力响应;[ Φ ]为结构的振型矩阵;{ q }为各阶振型的参与系数。
对于一个自由度为 s ,振型取前 n 阶的结构,即{ u }∈ ,[ Φ ]∈ ,{ q }∈ 。
对于分布参数体系,结构有无穷多个自由度。实际工程中一般根据精度需要,取结构的前几阶振型,控制振型参与质量系数在90%或者95%以上,将结构简化为有限自由度结构体系,之后通过合理布置传感器,对结构的动力性能进行检测。
模态置信矩阵法是基于模态可观测原则,要求传感器的监测数据应能够较好地反映结构受到激励后的动力反应信息,并使噪声等误差因素的影响尽可能减小。这就要求传感器布置所对应的结构实测振型矩阵[ Φ ]应具有良好的正交性。
[ Φ ]={ φ 1, φ 2, φ 3,…, φ n}
(2)
式中:{ φ i}为第 i 阶模态向量。则模态置信矩阵中的元素可表示为:
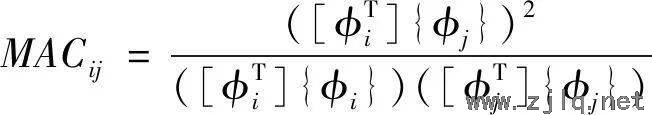
(3)
模态置信矩阵中元素代表第i阶振型模态与第 j 阶振型模态在欧氏空间中的空间交角余弦值。模态置信矩阵的对角线元素均为1,非对角元素为0~1之间的实数,且模态置信矩阵为对称矩阵。要保持实测振型的正交性,则需要使模态置信矩阵的非对角元尽量趋于0。
经试算分析,本文最终确定模态置信矩阵法适合采用逐步累加法进行迭代计算,具体计算步骤为:
2)根据工程经验以及结构振动特性或者采用模态动能法,选取一组初始传感器测点位置。初始测点数应少于预期测点数。根据式(3)计算出该组测点对应的模态置信矩阵并记录其对应的最大非对角元的值。
3)在剩余可选测点中选取一个测点增加到当前测点布置方案中,计算新测点方案对应的模态置信矩阵,同时记录模态置信矩阵中的最大非对角元。
4)更换所选取的待选测点,重复模态置信矩阵的计算步骤并记录最大非对角元。重复此步骤直至所有待选测点都被计算过。对比所有备选测点所对应的模态置信矩阵最大非大对角元,选择最小的模态置信矩阵最大非对角元对应的测点加入到当前测点布置方案中。
5)重复3)、4)步骤,直至传感器测点数及模态置信矩阵的最大非对角元满足要求。对于一些复杂结构,常以模态置信矩阵最大非对角元小于0.25作为基本优化要求,至此得到传感器的布置方案。
2
张弦梁结构传感器优化布置模拟
张弦梁结构是由预应力拉索、撑杆和上弦梁组合的典型的预应力结构,广泛应用于各种大跨度空间结构,该类结构往往需要布置结构健康监测系统。
由于张弦梁结构下弦为预应力拉索,结构整体刚度相对桁架较小,振动幅度较大,结构基频较小,适合采用振动模态分析进行结构健康监测。因此本文选择以张弦梁结构为例,按照模态置信矩阵法进行了传感器优化布置的试算。
2.1 张弦梁模型建立
本文选用SAP 2000软件进行建模计算。以跨度为60 m的张弦梁结构作为优化方法的试算模型。未施加预应力时张弦梁几何尺寸如图1所示,撑杆布置间隔为10 m。
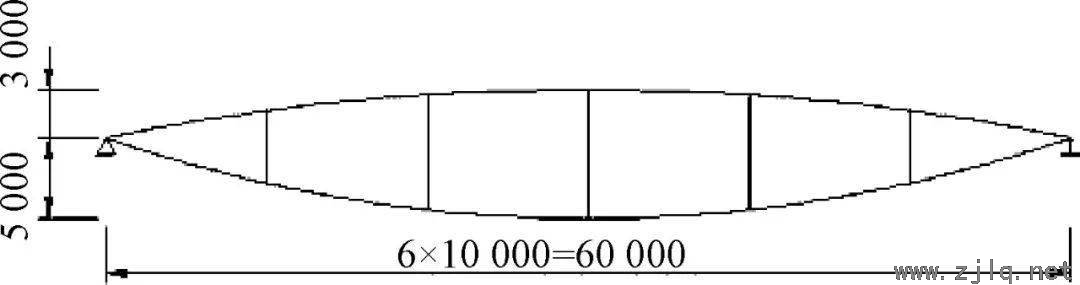
图1 张弦梁计算模型
上弦拱和撑杆选用Q345钢材,拱截面为400 mm×300 mm×12 mm箱形截面;撑杆截面为φ159 mm×6 mm圆钢管。预应力拉索材料为高强钢绞线,建模时采用等效截面积2940 mm 2。下弦索施加-60 ℃的温度荷载,对应预应力荷载400 kN。计算时,仅考虑自重荷载,由软件自动计算。同时,对结构平面外的自由度进行约束,结构仅在x-z平面内计算。
2.2 传感器布置要求确定
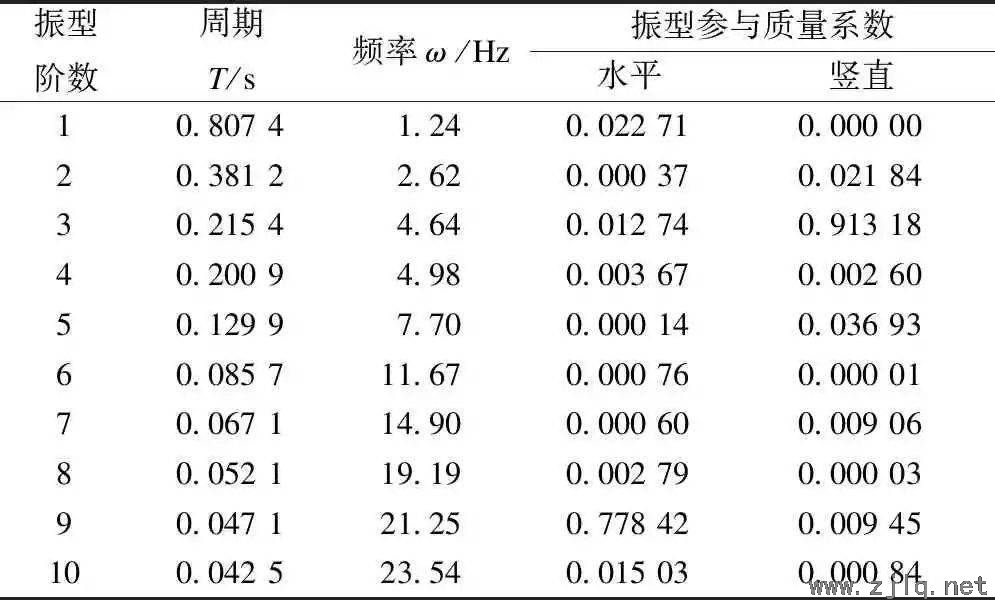
对张弦梁模型的动力特性进行计算。由于索的刚度远小于上弦拱的刚度,结构的部分振型表现为索的局部振动。忽略索的局部振动,仅考虑结构整体参与的振型,得到结构的前6阶振型模态如图2所示;结构前10阶振型的周期、频率、振型参与质量系数见表1。结构的前几阶振型以竖直方向振动为主,前5阶振型竖直方向的累计振型参与质量系数达到了97.5%。而水平方向的振型以第9阶振型为主,且前12阶振型水平方向的累计振型参与质量系数仅为85.7%。
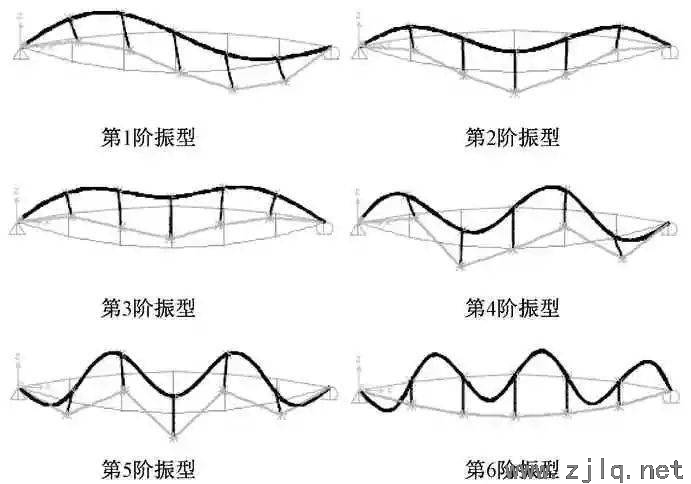
图2 结构前6阶振型模态
表1 结构动力特性
假定可布置传感器的测点仅分布在上弦拱上,所有测点位置及编号如图3所示。假定测点6受实际工程条件限制,无法布置传感器。传统方案中往往选取1~5、7~11号测点布置传感器,需要布置10个测点。基于以上模型与假定,应用模态置信矩阵法设计传感器布置方案。

图3 传感器布置位置及编号
2.3 传感器布置方案设计
初始测点选取2、4、8、10,每次迭代后的测点方案以及模态置信矩阵最大非对角元值见表2。模态置信矩阵最大非对角元随迭代次数的变化关系如图4所示。
表2 迭代运算结果
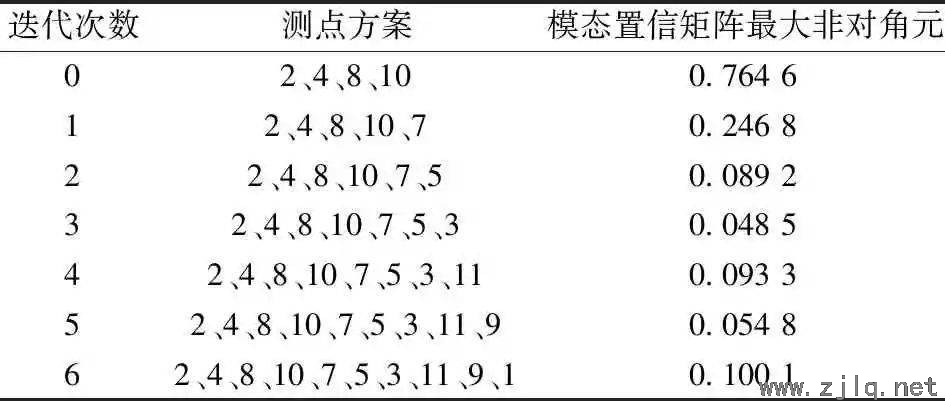
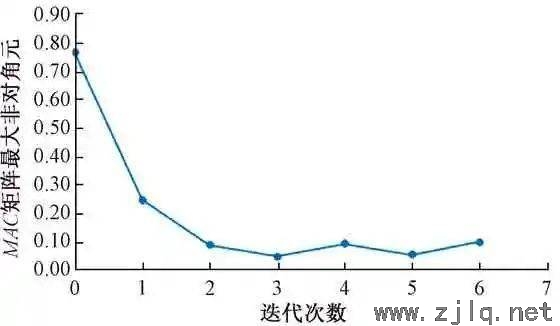
图4 最大非对角元随迭代次数的变化
根据图表数据分析可知,前3步迭代过程中模态置信矩阵的值迅速减小,而后趋于稳定,虽非单调递减,但均可以满足实际工程需要。综合考虑传感器数目和模态置信矩阵,最终传感器布置方案选取2、3、4、5、7、8、10 七个测点,对应的模态置信矩阵如式(4),可知,最大非对角元为0.0485。
[ MAC ]=

(4)
2.4 实施建议
根据算例分析过程,本文提出以下两点具体实施建议:
a.快速下降段。
此阶段模态置信矩阵有一个或多个较大的非对角元,无法满足实际工程需要。较大非对角元的个数取决于初始传感器测点方案的选取。好的初始方案应使得较大非对角元的个数尽量小。此阶段迭代过程中模态置信矩阵中较大非对角元的值迅速减小到能够满足工程需要的水平。
b.平稳阶段。
这一阶段模态置信矩阵的所有非对角元值均较小,随着迭代过程的继续,各个非对角元素的变化呈现不规则波动,且变化幅度较小,最大非对角元可能出现在任意位置,但均能够满足实际工程需要。
c.迭代末段。
由于待选传感器测点个数限制,迭代进行到最后几个测点时,无论选取哪个测点加入已有的测点方案,都会使模态置信矩阵的最大非对角元增大,此时增加传感器的数目反而会有负面作用,故应避免采用此阶段的迭代结果。
3
结 论
来源:亓玉台, 许庆. 张弦结构健康监测传感器布置优化方法[J]. 钢结构(中英文), 2020, 35(10): 29-33.