隧道工程在施工过程中经常受到地质条件和地形地貌等因素的制约,尤其是复杂的地质条件可能诱发的多种地质灾害,严重地影响工程施工进度,增加建设成本,甚至造成伤亡事故.常见的地质灾害有岩溶、断层、岩爆、突水、突泥、大变形、瓦斯等.隧道工程施工过程中进行超前地质预报,探明前方工程地质状况,进而指导隧道施工的顺利进行有着重要的作用(薛国强和李貅,2008).
目前我国用于隧道地质超前预报有多种方法,主要有隧道地震超前预报系统(TSP)、探地雷达法(GPR)、陆地声呐法、水平声波剖面法(HSP)、超前钻孔法等(宋先海等,2006;薛国强和李貅,2008).不同的方法有自身的适应性和缺陷.探地雷达法具有对施工影响、预报效率高等方面优势,但是在预报的解译和探测的深度方面存在不足.本文分析了基于有限差分法GPRMAX正演模拟的理论基础,讨论了二维FDTD法基本参数的选取,对隧道前方的不良地质体进行正演模拟得到反射图谱,并结合工程实例,说明该正演模拟能够指导解译工作.
1 GPRMAX正演模拟的理论基础
宏观来看,所有的电磁现象都可通过Maxwell方程组来描述,它由两个旋度方程和两个散度方程组成的,电磁波分为TEM、TM、TE三种模式.探地雷达中采用横磁模(TM型电磁波),TM波方程为(葛德彪和闫玉波,2011;郭立等,2012):
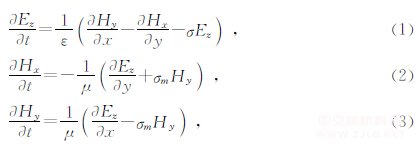
式中:ε为介质的介电常数;μ为磁导率;σ为电导率;σm为等效磁阻率,引入等效磁阻率其目的主要在于使方程具有对称性,在大多数电磁场问题中计算空间内不包含磁性介质,则有σm=0.
从上式可以看出,TM波只有Z方向电场强度Ez、X、Y方向的磁场强度Hx、Hy三个分量.运用Yee氏网格模型,利用中心差分代替对时间、空间坐标的微分,把连续变量离散化,推导出探地雷达正演模拟方程(李静等,2011;曾昭发等,2010):


2.1 空间步长的确定
用FDTD法对Maxwell方程进行数值计算时,在时域有限差分网格中,数值模拟的传播速度将随频率改变,导致非物理因素引起的脉冲波形畸变、人为的各向异性及虚假的折射现象,即出现数值色散现象,从而造成数值不稳定性(郭立等,2012).
二维空间中TM波的数值色散方程为
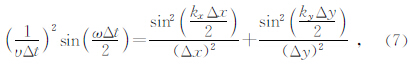
当Δt、Δx、Δy均趋于零时,色散可以减小到任意程度,但是由于计算机空间及速度等因素,决定时间步长和空间步长不可能无限的小,故选择合适的时间步长和空间步长不可避免.
根据文献(曾昭发等,2010),当时 ,相速度的最大误差为1.3%,当
,相速度的最大误差为1.3%,当 时,为0.31%,网格减小一倍,相位误差减小为四分之一.本文Δl取略小于
时,为0.31%,网格减小一倍,相位误差减小为四分之一.本文Δl取略小于 下的合适数据,选取原则是尽量降低Δl的有效小数数字长度,例如本文模型1中
下的合适数据,选取原则是尽量降低Δl的有效小数数字长度,例如本文模型1中 =0.036514837 m,Δl取0.03 m.
=0.036514837 m,Δl取0.03 m.
2.2 时间步长的确定
在FDTD中,通过按时间步推进计算空间内的变化规律,时间步长与空间步长之间必须满足一定条件,解的结果才能稳定,否则差分网格不稳定,随着时间步数的增加,计算结果也将无限制地增加.
二维空间中TM波的稳定性条件为

考虑到计算的简便性,探地雷达中取:

则:

时域差分法是在电磁场全部空间建立Yee矢网格计算空间的,但是由于计算机的存储空间都是有限的,在无限大网格空间中计算电磁场根本不可能,因此在计算中总是在某处把网格空间截断,使之成为有限空间(张鸿飞等,2009).网格截断处不引起波的明显反射,对向外传播的波而言就像在大空间传播一样.因此就需要在截断处设置某种边界条件,使传输到截断处的波被边界条件吸收而不产生发射,从而起到模拟无限空间的目的.
边界吸收条件发展经历从开始简单的插值边界条件,到后来广泛采用的Mur边界条件阶段,以及近二十年来发展的完全匹配层(PML)吸收边界阶段,随边界条件发展其吸收效果越来越好(葛德彪等,2011).在PML边界条件中,层的厚度通常有3~9个网格,本文边界层选取20个网格单元.
3 隧道超前地质预报数值模拟实例
根据隧道异常地质的特点,建立异常探地雷达探测正演模型,得到模拟的结果,为探地雷达进行超前地质预报的解译工作提供参考.
3.1 正前方含水溶洞模型
隧道掌子面正前方30 m处有一圆形含水溶洞,直径为0.5 m,如图 1a所示.取雷达频率为100 MHz,隧道介质的介电常数ε1=7.5,电导率σ1=0.00001 S/m;圆形溶洞中含水介质的介电常数ε2=81,电导率σ2=0.005 S/m;取网格的空间步长Δl=0.03 m,时间步长Δt=7.0711×10-11 s,时间窗口深度894 ns,迭代次数12635次,共模拟87道雷达波,模拟区域大小9 m×50 m,边界层厚度取0.6 m.
 |
图 1 含水溶洞模型及波形图Fig. 1 Water cave model and waveform figure |
通过模拟,得到雷达波形图如图 1b和c所示.其中b图为未去除直达波的反射剖面波形图,可以看出,由于直达波的影响,直达波信号几乎完全淹没了溶洞的回波信号.图 1c为经过零点平均、直达波置零方法去除直达波后的反射剖面波形图,可以看出,从30 m处开始,雷达波多次出现强烈反射,其后能量衰减明显.可推测该处地质异常,图形类似双曲线状,应为块状(或点状)异常,双曲线最高点应为异常点位置.
另外本文将模拟的数据利用Matlab转化成Mala格式,利用REFLEXW软件进行处理,实现数据处理工具之间的互补,如图 2所示为模拟数据利用REFLEXW软件显示的波形图,与图 1b比较可知,Matlab中显示的波形图与REFLEXW下显示的结果一致,但是REFLEXW显示的效果受到直达波的影响较小,其REFLEXW下探地雷达常规处理方法也较成熟和专业化.
 |
图 2 REFLEXW中显示的波形图Fig. 2 Waveform figure in REFLEXW |
隧道掌子面前方30 m处有圆形含水溶洞一角(半圆形),直径为0.5 m,如图 3a所示.共设置模拟88道雷达波,其余参数选取同3.1中模型.
 |
图 3 边界有含水溶洞模型Fig. 3 Border water cave model |
通过模拟,得到雷达波形图,如图 3b和c所示.可以看出,雷达波反射波形图与3.1中模型类似,但由于溶洞是在边界处,故其反射波形是双曲线的一部分,凸点处就是溶洞位置.
3.3 断层模型
隧道掌子面前方30 m处有一含水断层,断层水平方向厚度为10 cm(即两断层垂直厚度约为7.1 cm),倾角45°,如图 4a所示.共设置模拟87道雷达波,其余参数选取同3.1中模型.
 |
图 4 断层模型Fig. 4 Fault model |
去除直达波影响后得到如图 4b所示的波形图,观察可知,45°断层反射波形为弧线形,反射能量主要集中在断层位置处,振荡较少,而对于溶洞模型来说,其后为多次反射.
3.4 淤泥模型
隧道掌子面前方30 m处有一淤泥地带,设为一方形构造,倾角45°,边长1 m,如图 5a所示.共设置模拟87道雷达波,其余参数选取同3.1中模型.
 |
图 5 淤泥模型Fig. 5 Silt model |
去除直达波影响后得到如图 5b所示的波形图,可以看出,在淤泥处也形成多次连续明显的强反射,波形为双曲线,但是相对于3.1中模型,该模型多次反射间距离明显减小,信号衰减迅速.通过两者几何模型比较,在电磁参数相同的情况下,与异常体的几何形式及倾角有关系,结合3.3中断层模型,推断出水平方向倾角越小,异常体处能量衰减速度越快.
4 工程应用实例
如图 6为某地使用瑞典Mala探地雷达在隧道掌子面进行超前地质预报时经数据处理后得到的GPR图像,可以看出图中圆圈处的波形带有明显的双曲线特征,且随深度(向右)增加,信号振荡并逐渐减弱,判定为溶洞,后经工程施工证实该处判断正确,如图 7所示为该处现场图像.
 |
图 6 现场实测GPR图像1Fig. 6 GPR image 1 in project |
 |
图 7 工程现场Fig. 7 Engineering field |
如图 8所示,为另一处隧道掌子面超前地质预报GPR图像,可以看出图中圆圈处呈现双曲线波形,且迅速衰减,该处电磁信号频率较低,振幅强,存在大量的多次振荡,初步断定为含水量较大的岩溶或淤泥,因此给出施工在该处需注意安全的建议,后经证实该处为岩溶.
 |
图 8 现场实测GPR图像2Fig. 8 GPR image 2 in project |
如图 9所示,亦为隧道掌子面超前地质预报GPR图像,图中两条黑线为近似弧线线形,震荡较少,预估为裂隙发育,图中裂隙右侧区域信号杂乱,多处有双曲线状波形,推测为破碎区域,局部富水,后亦已得到验证.
 |
图 9 现场实测GPR图像3Fig. 9 GPR image 3 in project |
上述通过对现场应用实例的分析,印证了本文的模拟结果.反之,可以通过对探地雷达隧道超前预报的正演模拟的研究,指导工程的解译工作.但是需要注意的是由于工程实际情况复杂,介质为非均匀物质,其物性参数存在或多或少的差异等原因,因此造成工程中探地雷达图像显得杂乱,这就需要工程人员在解译过程中仔细观察图像,从中找出图像中的特征进行解译.
5 结 语
5.1 通过分析GPRMAX正演模拟的理论基础,利用中心差分代替微分,推导出探地雷达正演模拟方程.5.2 从降低数值色散现象,避免出现数值不稳定性出发,依据数值色散方程确定出FDTD法空间步长的基本参数;依据解的稳定性条件,确定基本参数时间步长;以及吸收边界层厚度的确定.
5.3 采用GPRMAX程序对正前方含水溶洞、隧道边界处溶洞、断层模型、淤泥模型进行了正演模拟,模拟结果表明:圆形含水溶洞产生双曲线弧线波形,双曲线最高点即为溶洞位置;断层射波形为弧线形,反射能量主要集中在断层位置处,振荡较少;不规则的淤泥模型也形成双曲线波形,但是信号衰减迅速.通过模拟以及工程验证,便于工作人员依据图形特征准确进行地质解译.
5.4 利用Matlab将模拟的数据转化成Mala格式,利用REFLEXW软件进行数据处理,结果一致,从而实现数据处理工具之间的互补.