From 孙利民 尚志强
原载于《桥梁》杂志2018年第4期
结构健康监测技术被广泛应用于大型桥梁的养护管理,但受数据分析方法和计算方式的限制,桥梁结构健康监测系统所积累的海量监测数据并未得到有效利用。近几年,大数据技术的发展为桥梁结构健康监测数据的有效利用带来了希望。大数据可视化分析是大数据分析的一个分支,能够实现高维数据可视化的同时,识别数据中的模式。
在传统的桥梁养护管理中,基于人工检测的结构状态评估扮演了重要角色,然而人工检测工作量大、主观性强,难以实现对结构性能的长期定量跟踪。近年来,结构健康监测技术(Structural Health Monitoring, SHM)在大跨桥梁的养护管理中得到广泛应用。桥梁结构健康监测通过在结构上安装传感器,以实时获取桥址环境和结构响应的信息,并基于这些信息对桥梁的技术状态做出实时、自动的评估甚至安全预警。我国当前至少有240多座大跨度桥梁安装了结构健康监测系统(Structural Health Monitoring System, SHMS),经过长期的观测,这些监测系统积累了大量的数据,基于这些数据有效解读结构的状态、识别可能的损伤,成为目前SHM研究的关键问题。
利用SHM数据进行结构状态评估和损伤识别有“基于模型”和“数据驱动”两类方法。基于模型的方法本质上是桥梁结构有限元建模、模型修正、系统参数反演的过程,对理论模型的精度和监测数据的质量有很高的要求,目前在实际工程中应用效果还不理想。数据驱动的方法关注监测所得到的输入和输出数据相关关系的变化规律,以识别结构状态所对应的模式,借助于成熟的统计学理论,数据驱动方法在SHM中得到广泛应用。但传统的统计方法由于计算能力和分析手段的限制,只能分析少部分、低维度的数据样本,且无法高效地呈现分析结果,因此尚不足以解决海量、高维SHM数据的分析问题。
大数据技术是近几年的新兴技术,已在互联网、电子商务、医学等领域得到广泛应用,改善了计算能力不足、数据分析方法低效等问题,在SHM的数据处理上也展现出广阔的应用前景。大数据可视化分析是大数据分析的一个重要分支,该方法将人所具备的、机器并不擅长的认知能力融入到分析过程中,可提升数据分析的效率和准确性,并可对高维数据进行直观的呈现。
“大数据”概念首次提出于1996年,2008年《Nature》杂志推出大数据专栏,2011年麦肯锡公司的研究报告对大数据的关键技术和应用领域等进行了全面的分析总结,大数据逐渐为各行各业所关注。“大数据”的内涵和外延在不断地被丰富,在不同的文献中,“大数据”被描述为数据集、可实现的功能、数据变现过程、架构和技术等。大数据应该从数据集特征、思维方式、技术三个方面进行理解(图1)。


一般认为,大数据具备4V特征,即数据体量大(Volume)、种类多(Variety)、增速快(Velocity)、价值密度低(Value)。4V特征并没有明确地限定大数据的体量规模,因而可广泛适用于各个行业。
大数据分析应具备的三个思维方式,即“使用全体数据进行分析”“接受数据混杂性,数据量大弥补质量差”“追求相关关系而非因果关系”。因而具有以下特点:与传统统计分析只使用一小部分随机抽样数据相比,使用全体数据可以发现更多的细节和有价值的信息;接受数据混杂、增大数据量能够简化分析模型并避免过拟合,从而获得更准确的分析结果;从相关关系切入则可为数据分析提供新的视角。当前大数据处理技术已使得分析所有数据成为可能,通过大数据分析挖掘相关关系也取得了许多成功应用;但以数据量大弥补质量差时,如果全部数据中的噪声多于信号则信号易被掩盖,因此不能盲目收入所有数据,仍需寻找与分析目的强相关的数据。
大数据的技术主要体现在数据采集、存储、计算处理、分析方法等几个方面。大数据的采集、存储、计算等多以软件工具的方式呈现,如用于获取数据的物联网、互联网,用以存储数据的Hadoop分布式文件系统、NoSQL数据库,用于数据计算的Hadoop生态圈、MapReduce、Spark、Storm、云计算等。大数据分析方法涵盖以各种术语所表示的数据分析方法,包括数据库知识发现(KDD)、数据挖掘、机器学习、模式识别、统计学等。这些术语虽然在应用领域和关注点上有所不同,但当前在大数据语境下,其间的差别可不必考究。
与大数据分析方法有关的另一个术语是人工智能,它是一个宏大的概念,它的提出远早于大数据。人工智能与大数据分析的主要区别是目标上的不同,前者是产生具有智能行为的东西,后者则用以发现数据中隐藏的知识。但二者都要靠大数据实体的支撑实现,且可以共用分析方法。当前人工智能的代表技术是深度学习,属于机器学习的一个子集,由于在图片、语音等识别问题中的出色性能,常脱离于机器学习被突出强调。
KDD、数据挖掘等同于机器学习,贯穿于大数据分析的整个流程,模式识别是其中的一个环节。大数据分析流程在KDD流程的基础上得到完善,强调了多源异构数据融合和特征提取的重要性,最终可由数据预处理、数据融合、特征工程、模式识别、可视化等环节构成。但应该注意到,这几个步骤之间的顺序并非绝对的一成不变,且有可能在某一步实现多个功能。
数据可视化在大数据分析流程中的功能是呈现数据分析的结果,当被直接用于探索数据、挖掘数据中的模式时也被称为大数据可视化分析。大数据的一个特征是数据种类多,在数据集中表现为数据的维度高。高维数据难以有效地可视化,且会引起数据分析中的维度灾难问题,即数据集在高维空间中分布稀疏,缺乏足够的数据构建模型。传统数据分析常以降维的方式减少数据集中的变量数,由此也会带来原始数据集中信息量的减少。大数据可视化分析为有效地呈现、分析高维数据提供了新的思路,在SHM的模式识别问题中也展现出应用的潜力。
平行坐标图法(parallel coordinate plot, PCP)、t分布随机邻域嵌入法(t-SNE)是当前高维数据可视化中常用的两种方法。t-SNE在高维空间中构建每个数据点对其近邻的概率分布,并在低维空间中重构该概率分布,通过最小化两个概率分布间的差距,以保证高维空间中的数据点在低维空间中具有相近的局部结构,最终将结果显示于二维或三维坐标图上。t-SNE虽然能有效探知原始数据的结构和分布,但需要很高的计算开销。与t-SNE相比,PCP不需要对原始数据进行降维显示,且具有更高的可视化效率。PCP通过N个平行坐标轴将N维数据投射到二维空间中,每个数据点被表示为PCP中的一条线段,由此原始的高维数据集可被表示为一个几何系统。PCP能够呈现数据间的相关关系,因而具有模式识别功能,这也体现了大数据“追求相关关系而非因果关系”的思维方式。PCP的模式识别功能由三个重要的可视化特征实现,分别为以下几方面——
线段夹角,表明变量间的正负相关关系,图3(a)中线段交汇于一点,表示两变量间具有强负相关关系,图3(c)中线段彼此平行,表示两个变量间具有强正相关关系。
线段交点区域,表明变量间相关关系的强弱,图3(b)线段交汇于一个区域,表示两变量间具有弱负相关关系。
线段分布,表明趋势模式或异常点模式。趋势模式对应密集区域的线段,异常点则是稀疏区域的线段。图3(d)下方的线段可判断为趋势,上方的线段为异常点。

PCP用于大数据集时,线段数量的增多会造成线段间的重叠、遮挡(图4),从而掩盖坐标图中的可视化特征。为消除线段重叠、减少视觉混杂,学者们提出了各种改进的PCP方法。基于Alpha混合的PCP方法较早地被提出,其将PCP中的每条线段赋予较低的透明度,使线段稀疏部分的颜色被淡化、线段密集区域的颜色被加深。此种方法的缺陷是透明度值存在下限,不能扩展到更大规模的数据集中。基于分布直方图的PCP方法(图10)按每两个变量计算二维分布直方图,以直方图中的每一格表示坐标图中的一条线段,并按直方图的频率值设定线段的透明度。由于能在大幅减少线段数量的同时,保留PCP中的可视化特征,基于分布直方图的方法可被扩展到更大规模的数据集。除此之外,PCP中减少视觉混杂的方法还有基于捆扎的方法、基于聚类的方法、基于刷的方法等。



桥梁SHM的监测内容主要包括环境运营荷载与结构响应两类,环境与运营荷载的监测项有温度、降水量、空气湿度、风荷载、交通荷载、地震输入等;结构响应监测项有几何变形和位移、加速度、应变、转角、索力等。基于SHM数据首先可以进行结构损伤或异常识别,但在实际桥梁中这还很难理想实现,一是因为当前国内安装有SHMS的大部分桥梁服役时间较短,尚未出现明显的损伤和退化;二是受传感技术和数据分析方法的限制,结构初期的微小损伤难以被识别。进行结构状态评估是SHM的主要目的之一,对于服役初期阶段尚无明显损伤的新结构,SHM数据可用于分析正常环境与运营荷载下的结构响应规律,从而定义结构的正常状态,并分析结构状态发生偏离的原因。与结构状态评估有关的研究还包括荷载效应分析、可靠度分析、安全预警、传感器故障识别等。
在数据驱动的方法下,桥梁结构损伤或异常识别与状态评估大都可归类于模式识别问题。传统数据驱动的分析中,模式识别前一般要先对多通道、多种类的传感器时间序列数据进行降维,以提升机器学习方法的效率和准确性。然而降维存在定阶的问题,即需要确定最终的变量个数,尽可能多地保留原始数据中的信息。此外,损伤识别、传感器故障识别等问题常缺乏足够的标注数据,使得有监督学习方法很难被应用;无监督学习虽不使用标注数据但对参数设定敏感,且很容易陷入局部最优解。PCP将人的认知能力融入到数据分析中,为无法使用有监督学习及无监督学习不稳定情况下的模式识别提供了新的思路,并可直接对原始高维数据进行可视化。本文中,PCP在SHM模式识别中的性能将通过2个数据集验证,这两个数据集均取自某斜拉桥的健康监测系统。该斜拉桥共布设有169个各种类型的传感器,可实现对环境荷载与结构响应的长期实时监测。

第一个数据集取自2007年,包括四个数据维度,分别表示设置在主梁伸缩缝处的两个伸缩仪(DP001,DP002)和跨中钢箱梁腹板、底板位置的两个温度计(ST002,ST009)所测的17520条数据。两个伸缩仪在安装时因对梁体的热膨胀考虑不足而没有设置足够的预张量,使得夏天高温时段的伸缩仪监测值溢出其量程而不再发生明显变化。发生故障的两个伸缩仪中,DP001在高温时段过后恢复工作,DP002则自此一直处于故障状态(图8)。除了正常变化状态和伸缩仪故障两种模式,时程图上以0值出现的离群点构成了另一类数据模式,其由供电中断等临时性故障引起,可被视为数据中的噪声。PCP被用以识别这三种模式,为避免数据量增大产生的线段重叠问题,在此分别使用了基于Alpha混合(图9)和基于分布直方图的PCP方法(图10)。


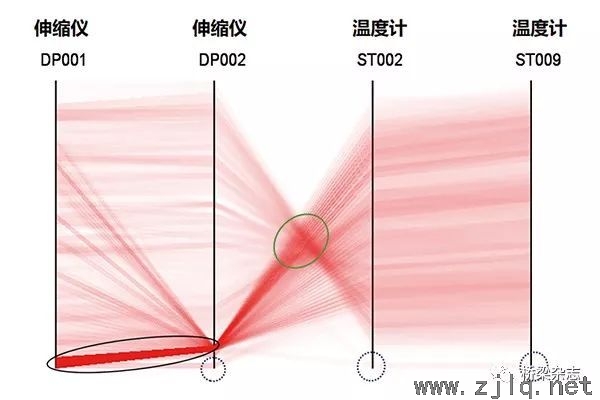
通过基于Alpha混合的PCP可以明显地识别数据集的三种模式。正常状态的数据表现为两个伸缩仪间、两个温度计间大部分平行的线段,表明变量间具有正相关关系;伸缩仪与温度计之间的交汇区域(绿色圈内)则表明了二者之间的负相关关系。在两个伸缩仪对应的坐标轴底部均有密集的线段区域呈现较深的颜色(黑色圆圈内),对应着伸缩仪在夏天高温时段的故障。在深颜色区域中,DP002伸缩仪线段比DP001伸缩仪更为密集,颜色更深,对应着DP002处于失效状态的时间更长。在4个坐标轴最下方区域还存在一些远离趋势的线段,即异常点模式(蓝色虚线圈),对应着数据中的噪声点。基于Alpha混合的方法已可明显地识别出数据集中的3种模式,相比之下,基于分布直方图的PCP则可更为突出地显示所关注的伸缩仪故障数据。
上面讲到的第一个数据集中,正常状态、传感器故障、噪声等模式是事先已知的。而本节第二个数据集中可知的仅有正常状态的模式,PCP被用以探索该数据集中是否还隐藏有未知的模式。第二个数据集有7个变量,分别代表结构一阶振动频率(竖向弯曲、横向弯曲、扭转)、温度、风速、交通、湿度、交通荷载,其中交通荷载由该斜拉桥跨中所测加速度的均方根值(RMS)表征。该数据集的时间跨度长达5年,按每小时一个数据点的频率计算得到了由2007年至2012年共52608条数据。为研究环境与运营荷载对结构动力特性的影响规律,各变量之间的相关系数也分别被计算,并显示在图11、图12中PCP的下部。在该数据集的模式识别中同样使用了基于Alpha混合(图11)和基于分布直方图(图12)的方法。


基于Alpha混合方法的PCP中,风速与扭转频率、竖弯频率的平行坐标轴之间各存在两个狭长的深色区域(蓝色圆圈),可表明两个变量间具有一定的正相关关系。这两个变量与风速的相关系数分别为0.199和0.132,则可推断该相关系数很大程度上由PCP中的狭长深色区域解释。同理,由在竖弯频率与温度、横弯频率与交通荷载坐标轴间识别到的深颜色交汇区域(绿色圆圈),也能很大程度上解释这两组变量间的负相关系数。除了表示正相关关系的狭长形深色区域和表示负相关关系的交汇区域,还可在图中识别到一些表现为细条形的模式,如交通荷载和横弯频率坐标轴间黑色圆圈中所示。上述由PCP可视化特征识别的相关关系仅对应着数据集中的一部分数据,在此将其定义为“局部相关关系”。局部相关关系模式所具备的物理意义当前尚无法解读,有待于通过交互式的PCP方法提取出来作进一步的分析。
由于数据量较大,基于Alpha混合的方法必须设定很小的透明度值(在此为Alpha=0.001)。但Alpha值在绘制PCP的OpenGL(绘制计算机图形的函数库)中不可能无限小,在更大规模的数据集中,该方法仍将受到线段重叠的影响而无法使用。基于分布直方图的PCP方法中,线段数量取决于分布直方图的数量,可不受透明度下限值的影响。采用分布直方图方法的图12中交换了部分坐标轴的顺序,仍可以识别线段交汇的深色区域、细条形深色区域所表示的局部相关关系,但对狭长形的深色区域呈现不够明显,这与该模式的特征不明显有关,也说明在绘制PCP的过程中应结合使用多种参数(直方图数、透明度等),以更全面地识别可能被遗漏的模式。
在桥梁结构健康监测领域,深厚的力学背景虽决定了对桥梁结构机理和行为较高程度的认知,但实测数据中仍存在环境与运营荷载、采集设备故障等所产生的不确定性因素。认知这些不确定性因素、从中识别隐藏的模式,并合理解释其对应的物理现象,是采用包括可视化分析在内的大数据分析方法应试图去解决的问题。
本文介绍了在大数据可视化分析中常用的PCP方法,通过某斜拉桥结构健康监测系统所采集的两个数据集,对其数据可视化和模式识别功能的适用性进行了验证,可得到以下结论:
(1) PCP方法可用以识别传感器故障引起的数据异常,基于分布直方图的PCP方法能够更为突出地显示该种模式。
(2) PCP方法中的趋势模式可呈现环境荷载与结构响应之间的局部相关关系,且能够反映大数据分析“追求相关关系而非因果关系”的思维方式。
(3) 与局部相关关系模式对应的数据有必要被提取出来以进一步的分析,能够选择并提取相应线段的交互式PCP方法仍有待于在后续研究中被开发。
大数据方法在结构健康监测数据分析中的应用研究才刚刚开始,桥梁结构是遵循力学原理设计出的一个人工产品,相应的监测数据具有明显的“工业大数据”特征,在借鉴其他领域的大数据分析方法时,我们也应十分注意方法的适用性,避免步入误区。