摘 要:以位于季冻区内的河北省张承高速路基填土为研究对象,在设计满足实际工况下的冻融循环的试验基础上,采用室内动三轴试验,分析不同影响因素包括冻融循环次数、压实度、围压及振动频率下各项动力学参数的变化情况,应用多元非线性回归的线性化分析方法,建立动黏聚力与最大动弹性模量的回归公式,识别路基填土在冻融循环作用后的动载作用下的动力学特性变化规律,为解决季冻区高速公路路基填土冻融病害提供相关数据和理论支持。
关键词:冻融循环;高速公路;路基填土;动力学;动三轴试验;
作者简介:李博楠(1994-),男,硕士,主要研究方向:道路工程材料。;
张家口—承德高速公路地处河北省北部,属季冻区域,随着冬奥会的来临,作为首都环线的重要组成部分,其通行量日益提高,而气温的变化尤其是冻融作用引起的路基路面病害也越来越严重,路基因冻胀、融沉而导致的直接或间接病害影响了高速公路的服务水平和通行质量,加大了养护维修成本,有必要对张承高速公路的路基填土在冻融循环作用及行车动荷载作用下发生的强度、变形等物理力学特性展开相关研究。
高速公路路基在经受冻融循环作用时,不仅承受着内部的温度应力和上部的自重静载,还要承受来自过往车辆行驶所带来的动荷载。研究路基填土在冻融循环作用及动载作用下的动力学特性,对进一步了解土体在冻融循环作用下的实际力学行为具有非常重要的意义。
选取位于张承高速沿线具有一定代表性的土样,采用液塑限联合测定仪进行液塑限的测定,根据塑性图法对本次试验土样进行工程分类的判定,确定本次所选择土样的液限为31.2%,塑性指数Ip为13.2,落在A、B交点的左上方即CL区,因此可以判定本次试验用土样为低液限黏性土。
选择落锤式电动击实仪的方法进行试验,采用重型击实,分五层每层27击。取均匀性良好的试验用土样5组,按照相邻含水率之差2%~4%的要求分别配置成不同含水率的土样试件进行试验。确定最佳含水率为11.2%,最大干密度为1.95。
结合张承高速路线沿线气候变化规律,拟定环境负温-10℃,融化时温度统一设定为20℃。考虑实际工况,土体的冻结过程主要为单向冻结,为更接近工程实际,将制备好的最佳含水率下的土样试件用塑料薄膜包裹后放置在带有孔位的泡沫塑料板中模拟土在路基中受冻时的物理状态,将土样与泡沫板一同放入冷冻箱及恒温箱中进行试验操作。结合当地的实际昼夜温度变化及冻融情况,选择冻结—融化时间周期为24h, 其中冻、融分别取12h。对冻融次数选择分别为1次、3次、5次、7次和11次。
为讨论不同层次或不同密实程度下土基受冻融作用影响的变化情况,选择压实度92%、95%、98%分别进行正交试验。
采用TAJ-20型电液伺服动(静)三轴试验仪。本次试验采用三种振动频率f=0.5Hz、f=1Hz、f=5Hz的正弦波的形式输入,同时为简化操作,选择动力加载方式为单向加载,当动应变累计达到5%时停止。
各组试验的具体参数如表1所示。
表1 试件各项条件指标
各组试件均在30、60和90kPa围压水平下进行试验。围压的加载增速设定为1kPa/s, 待围压增至目标值后,调整正向应力使其与围压相同,待试件在等压条件下固结24h后关闭排水阀;在不排水条件下沿试件轴向施加σd偏应力,然后施加同样值的动应力半正弦波进行动力加载。
以破坏振动次数Np=100次、1000次和10000次为研究条件,通过动强度曲线确定各破坏时振动次数Np和对应的动应力幅值σd,绘制摩尔应力包线,确定土样的动摩擦角和动黏聚力cd。
同一压实度(K=95%)、同一振动频率(1Hz)不同冻融循环次数下动强度指标cd 、φd值如图1至图2所示。
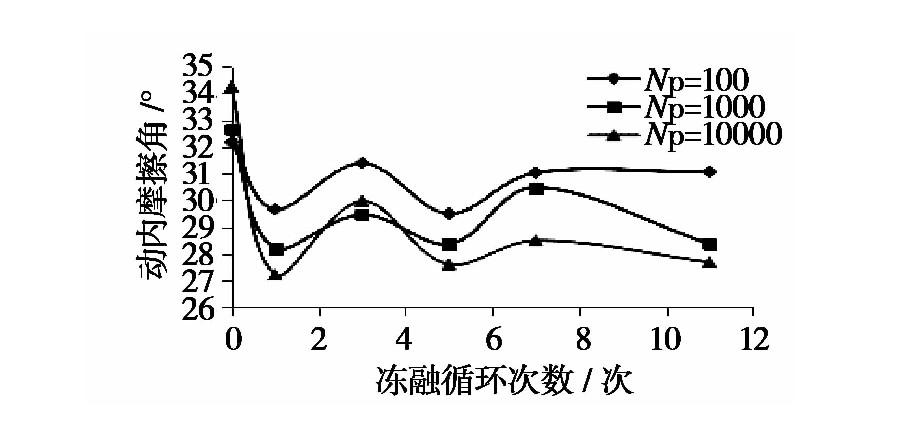
图1 动内摩擦角与冻融循环次数关系曲线
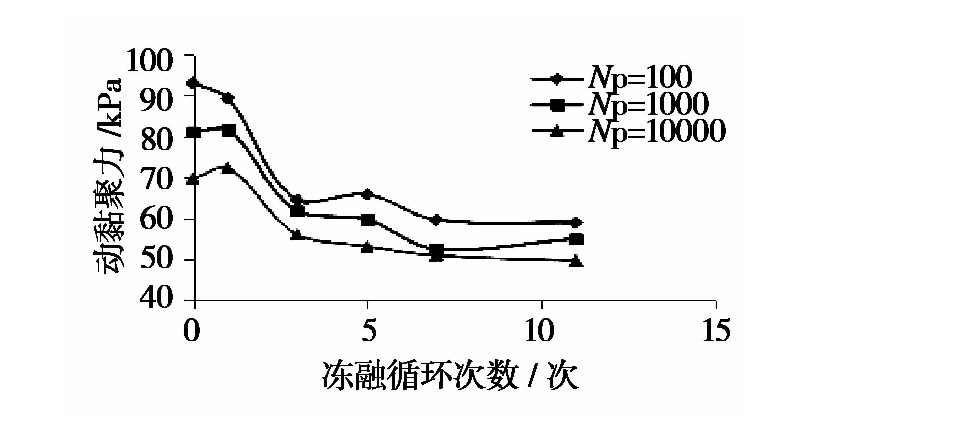
图2 动黏聚力与冻融循环次数关系曲线
试件在经受第1次冻融循环作用后,其动内摩擦角均有一定程度的下降,而后随着冻融循环次数的增加,内摩擦角在27°~32°间波动。当处于同一冻融循环次数时,随着破坏振动次数的增加,动内摩擦角有一定程度降低;而随着冻融循环作用次数的增加,动黏聚力值逐渐衰减并趋于稳定,由于土样试件内部在经受第1次冻融循环作用,内部孔隙结构发生了趋于特征化的重新分布,在外部振动加载作用的影响下,孔隙结构被填充或压密,而在冻融循环作用次数继续增加后,孔隙结构再次被冻胀—水分排出作用改变或影响,内部土粒间作用力持续降低。
不同压实度下土样的动强度指标分别如图3至图4所示。
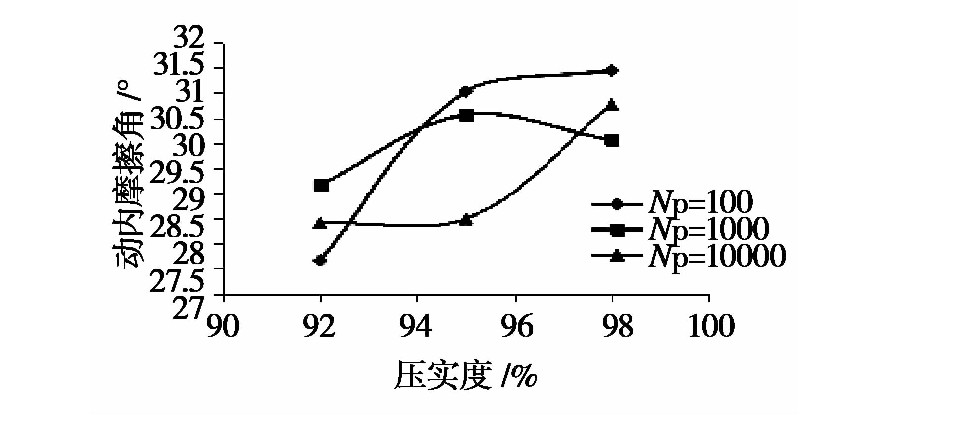
图3 不同压实度下动内摩擦角值
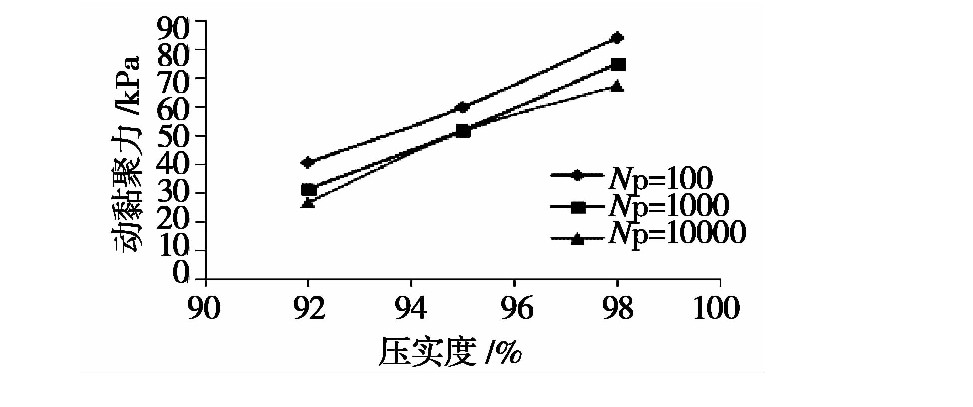
图4 不同压实度下动黏聚力值
不同压实度下内摩擦角曲线变化规律性较差;而动黏聚力随压实度变化的规律性较强,随着压实度的提高,动黏聚力类似线性增长。当试件的压实度一定时,随着破坏振动次数的增加,其动黏聚力有所降低。
不同振动频率下土样的动强度指标分别如图5至图6所示。
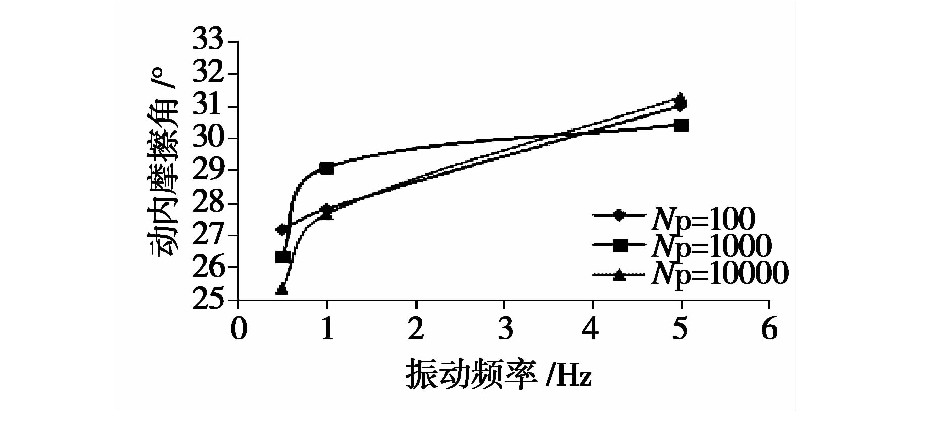
图5 不同振动频率下动内摩擦角值 下载原图
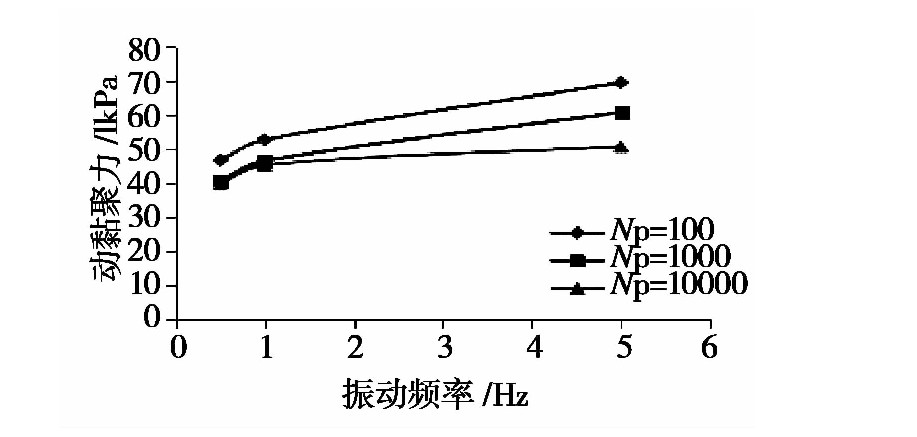
图6 不同振动频率下动黏聚力值
随着振动频率的增加,试件的动内摩擦角值与动黏聚力值均呈现上升的趋势,但随着振动频率的逐渐增加,变化趋势逐渐放缓。当处于同一振动频率时,随着破坏振动次数的增加,动摩擦角的规律性较差,而动黏聚力则是随破坏振次的提高而降低。
将动力加载第10次的循环时的动应力—应变曲线定为该动应力幅值下的滞回圈,通过椭圆拟合,以椭圆两顶点的连线斜率定为该动应力幅值下的动弹性模量Ed,而土体在受到循环荷载作用下,其动本构关系符合式(1)所列出的双曲线关系即:
Ed=σdεd=1a+bεd (1)Ed=σdεd=1a+bεd (1)
其中:
σd为动应力幅值/kPa;
εd为动应变/%;
a、b均为土体参数。
由式(1)又可导出:
1Ed=a+bεd (2)1Ed=a+bεd (2)
由于各条件下的动弹性模量值可由试验结果计算得到,因此只要通过对1Ed1Ed进行不同条件下的线性拟合,就能够确定不同条件下的土体参数a、b,在式(2),εd恒小于1,因此最大动弹性模量即为:
Edmax=1a (3)Edmax=1a (3)
各条件下最大动弹性模量曲线分别如见图7至图9所示。
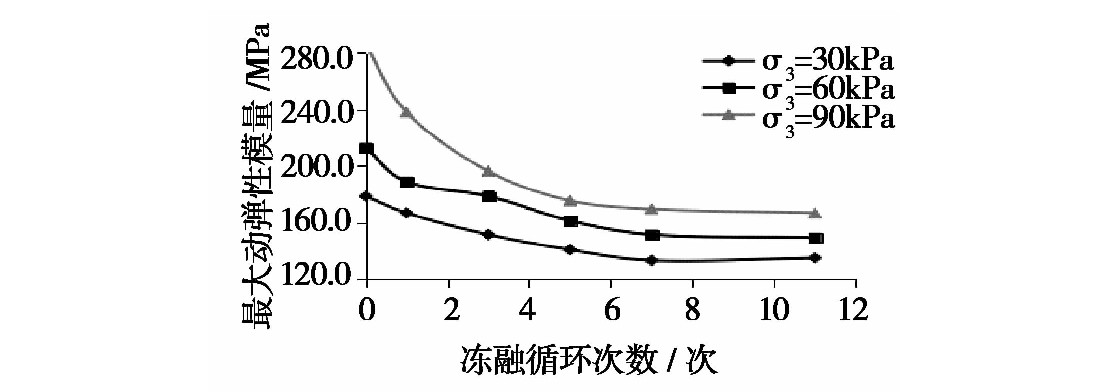
图7 不同冻融循环次数下最大动弹性模量曲线
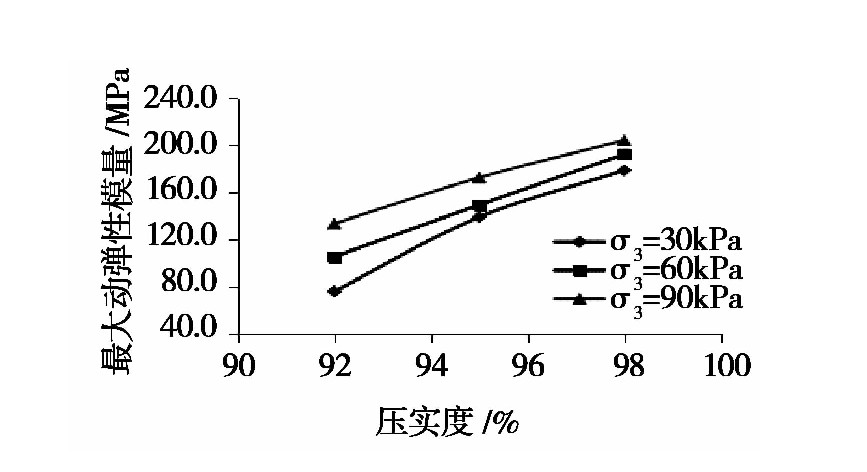
图8 不同压实度下最大动弹性模量曲线
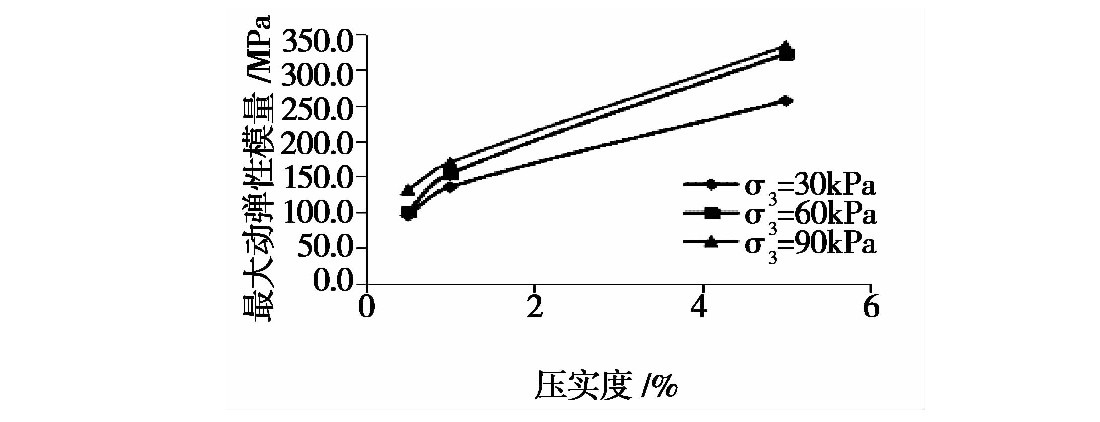
图9 不同振动频率下最大动弹性模量曲线
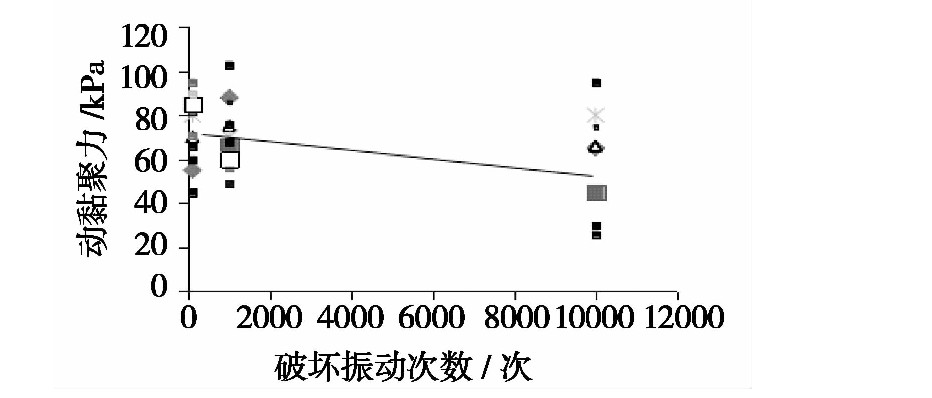
图10 单一考虑破坏振次下的动黏聚力标准值曲线
随着围压水平的增加,试件经受不同冻融循环作用次数下的最大动弹性模量均随之提高;当围压水平一定时,试件的最大动弹性模量随冻融循环作用次数的增加而降低,且当冻融循环作用次数为3次时,衰减速率达到最大,当冻融循环作用次数大于5次后,试件的最大动弹性模量逐渐趋于平稳;随着压实度的提高,试件最大动弹性模量显著增强;而在不同围压水平下,压实度的提高对试件最大动弹性模量的变化影响有一定的变化,随着围压水平的提高,压实的提高对试件最大动弹性模量的提升作用减弱;随着振动频率的提高,试件的最大动弹性模量增大。
以单一受破坏振动次数影响下的动黏聚力拟合值作为标准值,将其他各因素的试验值与标准值之比作为个参数下的代表值,采用比值法进行验证。
拟合曲线:
cd0=p1Np+q1 (4)
其中:
cd0为动黏聚力标准值;
Np为破坏振动次数/次;
p1、q1为拟合参数(分别为:p1=0.0013,q1=67.772)
冻融循环次数影响下的动黏聚力代表值拟合曲线(图11):
cN=cdcd0=p2+q2e−m2Np (5)cΝ=cdcd0=p2+q2e-m2Νp (5)
其中:
cN为冻融循环次数影响下动黏聚力代表值;
p2、q2、m2为拟合参数(分别为:p2=0.813,q2=0.447,m2=0.362)
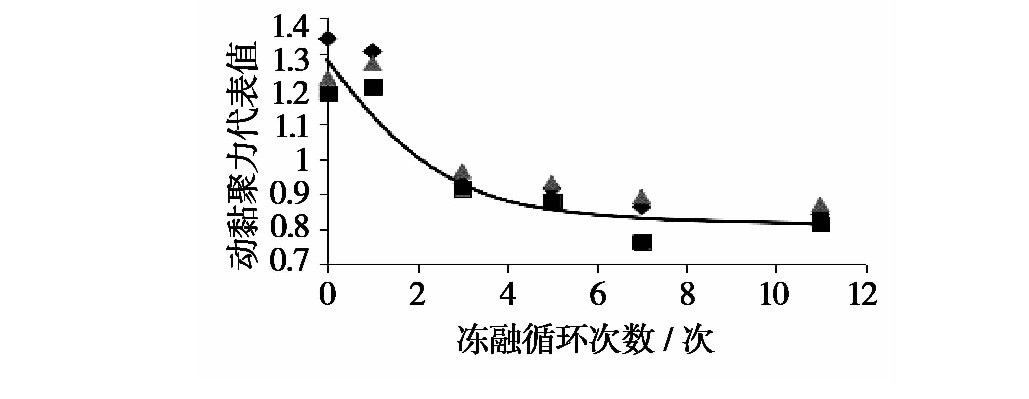
图11 冻融循环次数影响下动黏聚力代表值拟合
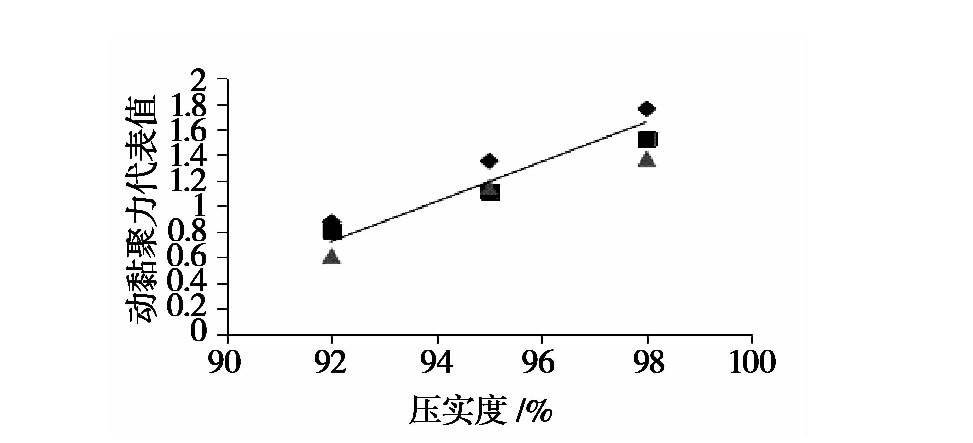
图12 压实度影响下动黏聚力代表值拟合
压实度影响下拟合曲线(图12):
cK=cdcd0=p3ln(K)+q3 (6)cΚ=cdcd0=p3ln(Κ)+q3 (6)
其中:
cK为压实度影响下动黏聚力代表值;
p3、q3为拟合参数(分别为:p3=12.015,q3=55.218)。
振动频率影响下拟合曲线(图13):
cf=cdcd0=p4f2+q4f+m4 (7)cf=cdcd0=p4f2+q4f+m4 (7)
其中:
cf为考虑振动频率下的动黏聚力代表值;
p4、q4、m4为拟合参数(分别为:p4=-0.215,q4=0.113,m4=0.676)。
考虑多重影响因素下的动黏聚力拟合公式可采用多元非线性回归的线性化分析方法进行计算:
cn=pcNcd0+qckcd0+mcfcd0+n (8)
其中:
cn为考虑各项因素后的动黏聚力拟合值;
p、q、m、n为调整系数(分别为:p=0.731,q=0.699,m=0.105,n=54.118)。
动黏聚力的拟合值分布情况如图14所示。
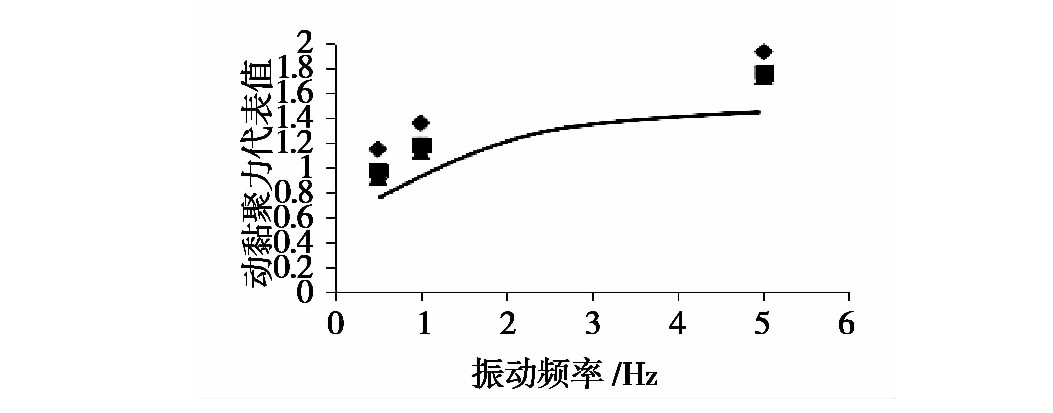
图13 振动频率影响下动黏聚力代表值拟合
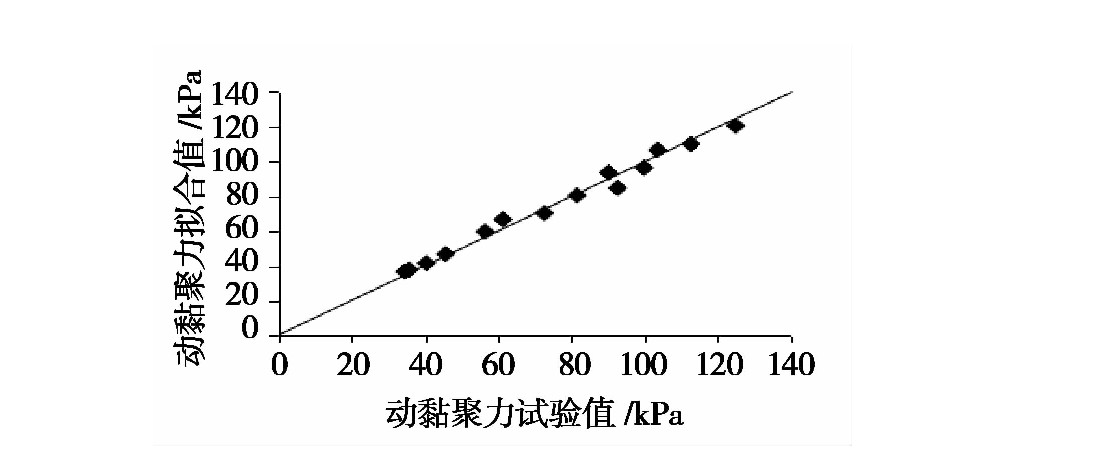
图14 动黏聚力的拟合对照验证
可以看出,拟合后的动黏聚力值分布在等值线附近,说明拟合效果良好。
单一考虑围压条件影响下的最大动弹性模量拟合值作为标准值,将不同条件影响因素下的试验结果与该值之比作为该种影响因素下的最大动弹性模量代表值,并对代表值进行非线性拟合。
Ed0=l1σ32+j1σ3+i1 (9)
其中:
Ed0为单一考虑围压作用下的最大动弹性模量标准值/kPa;
l1、j1、i1为拟合参数(分别为:l1=0.0031,j1=0.460,i1=133.571)
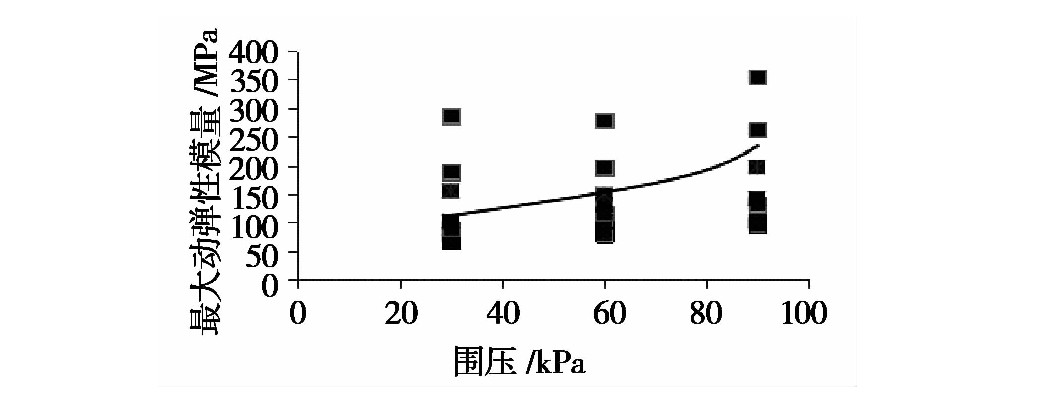
图15 单一考虑围压作用下拟合曲线
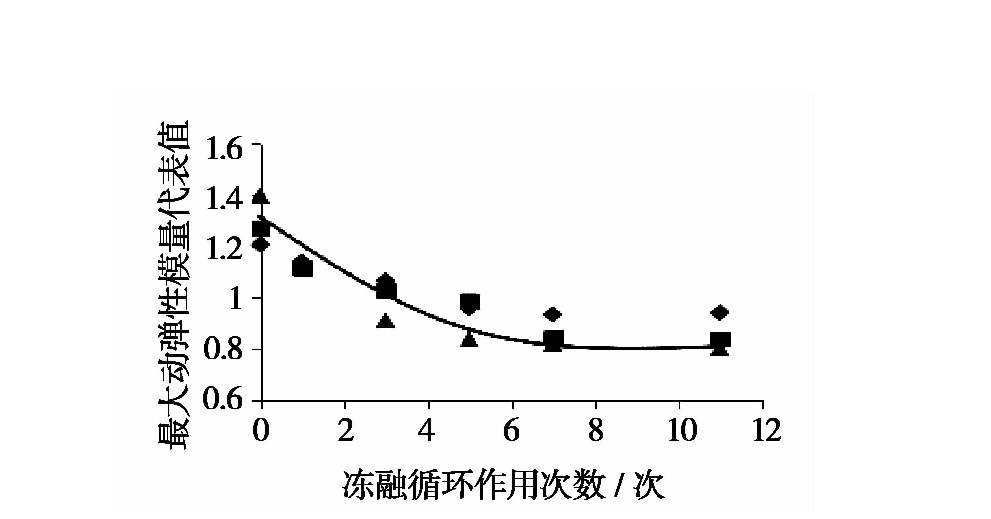
图16 冻融循环作用次数影响下最大动弹性模量代表值拟合曲线
冻融循环次数影响下的最大动弹性模量代表值拟合曲线:
EdN=EdmaxEd0=l2+j2e−i2Nft (10)EdΝ=EdmaxEd0=l2+j2e-i2Νft (10)
其中:
EdN为考虑冻融循环作用次数下的最大动弹性模量代表值;
l2、j2、i2为拟合参数(分别为:l2=0.850,j2=0.416,i2=0.392)。
压实度影响下最大动弹性模量代表值拟合曲线:
EdK=EdmaxEdo=l3ln(K)+j3 (11)EdΚ=EdmaxEdo=l3ln(Κ)+j3 (11)
其中:
EdK为考虑压实度影响下的最大动弹性模量代表值;
l3、j3为拟合参数(分别为:l3=12.561,j3=57.330)。
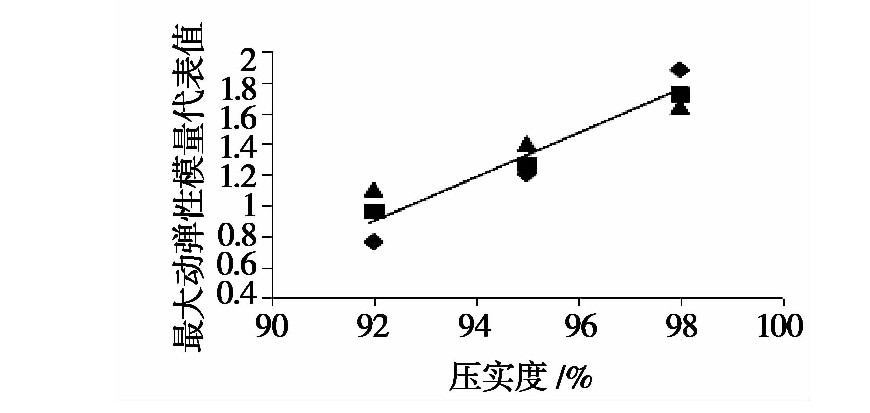
图17 压实度影响下最大动弹性模量代表值拟合曲线
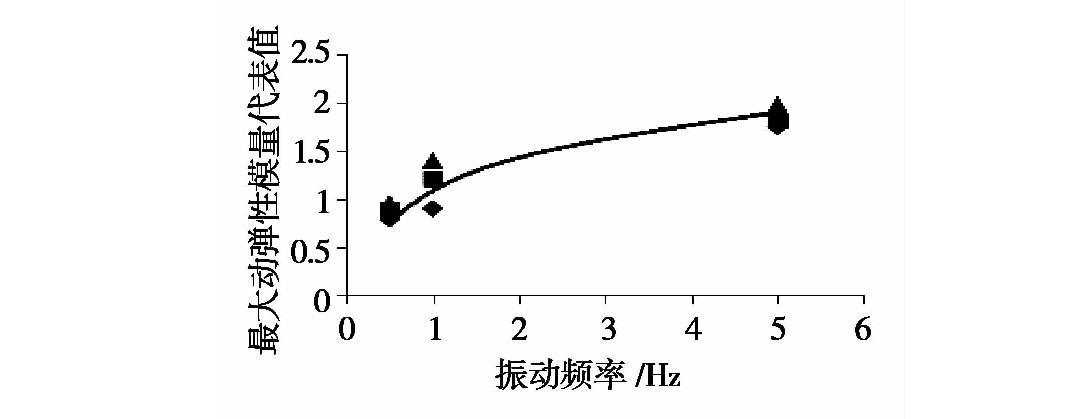
图18 振动频率影响下最大动弹性模量代表值拟合曲线
曲线用下式进行拟合:
Edf=EdmaxEd0=l4f2+j4f+m4 (12)Edf=EdmaxEd0=l4f2+j4f+m4 (12)
其中:
Edf为考虑振动频率影响下的最大动弹性模量代表值;
l4、j4、m4为拟合参数(分别为:l4=-0.262,j4=0.815,m4=0.368)。
考虑多重影响因素下的最大动弹性模量拟合公式可采用多元非线性回归的线性化分析方法进行计算,采用下式进行拟合:
Edn=l'EdNEd0+j'EdKEd0+p'EdfEd0+q' (13)
其中:
Edn为考虑各因素下的最大动弹性模量拟合值;
l'、j'、p'、q'为调整系数(分别为:l'=0.751,j'=0.363,p'=0.142,q'=-76.381)。
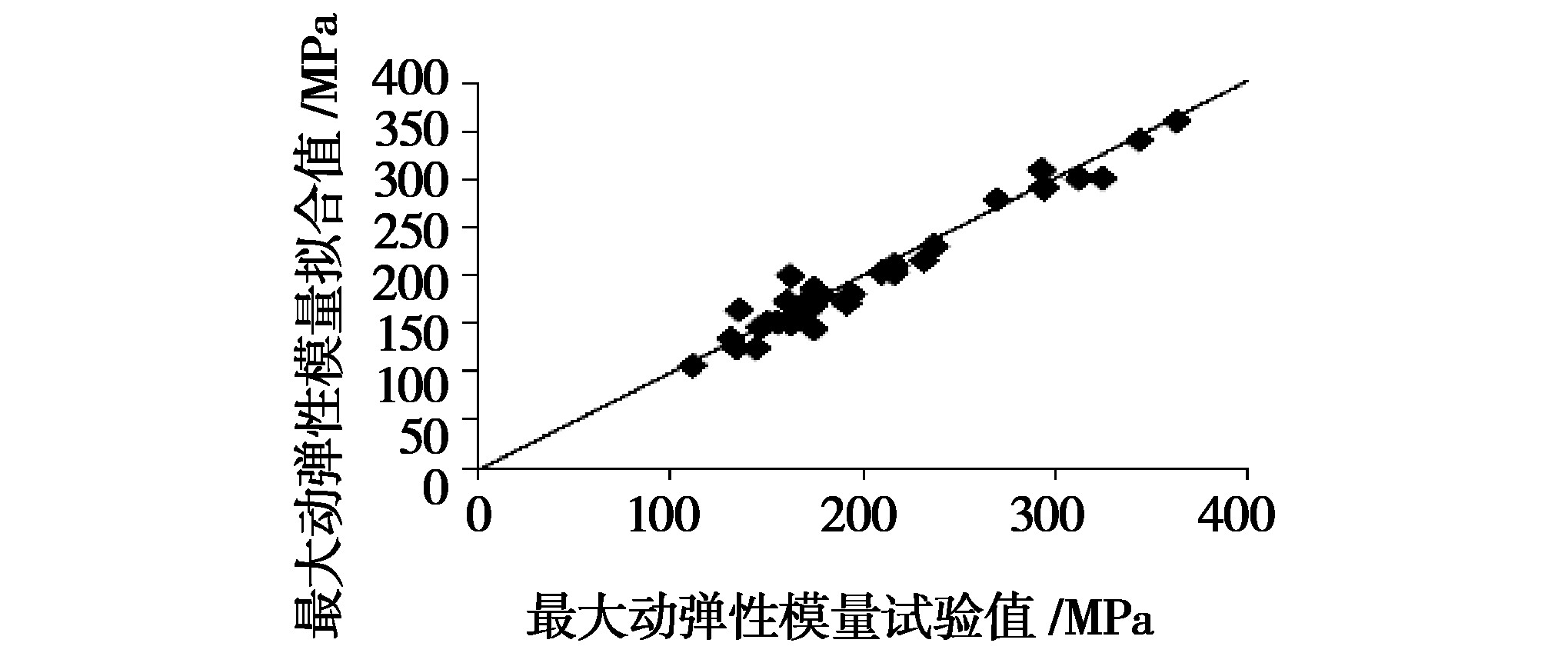
图19 最大动弹性模量的试验值与拟合值对照验证
最大动弹性模量经式(13)拟合后的取值与试验值对照大多均匀分布在等值线两侧,说明本次针对最大动弹性模量的拟合结果良好。
研究了不同冻融循环作用次数、不同压实度以及不同加载振动频率下试件的各项动力学参数的变化规律,并对不同影响因素下的动力学参数包括动黏聚力和最大动弹性模量进行多元非线性回归的线性化分析,提出了动黏聚力和最大动弹性模量的经验公式,直观地展现出不同影响因素下张承高速所在区域即河北省北部、北京西北部地区季冻区路基填土受冻融循环作用下的变形特性和强度变化规律,了解各个影响因素作用的强弱,推测各个力学参数在实际变化中的规律和趋势,为张承高速及国内类似季冻区域高等级公路的建设和运营和维护工作提供参考。
[1] 宋金华,李博楠,王亮,等.冻融循环作用下石灰改良土路基填料的动力特性研究[J].重庆交通大学学报(自然科学版),2018,37(2):47-54.
[2] 魏盛昊.冻融作用下路基填土力学特性及变形预测研究[D].西安:西安科技大学,2020.
[3] 夏梦露.冻融循环作用下路基土变形特性及数值计算分析[D].长春:吉林大学,2020.
[4] 陈洪兴,陈景龙.季冻区路基土抗剪强度指标变化规律研究[J].公路交通技术,2016,32(1):1-5.
[5] 王静,刘寒冰,吴春利,等.冻融循环对不同塑性指数路基土动力特性影响[J].岩土工程学报,2014,36(4):633-639.
[6] Yarbasi N,Kalkan E,Akbulut S.Modification of the geotechnical properties,as influenced by freeze-thaw,of granular soils with waste additives[J].Cold Regions Science and Technology,2015,48(1):44-54.
[7] 王威娜,支喜兰,毛雪松,等.冻融循环作用下路基土回弹模量试验研究[J].冰川冻土,2010,32(5):954-959.
[8] 陈文.季节性冰冻区公路路基湿度与模量研究[D].武汉:武汉工业学院,2012.
[9] 侯恩创.冻融循环对路基土物理力学性质影响的研究[D].哈尔滨:东北林业大学,2009.
[10] 李晶.对季冻区路基强度及稳定性的试验研究[J].黑龙江交通科技,2010,33(3):54-55.