0 引言
近几十年来,国内外许多学者致力于箱形梁桥的研究,分别从解析法、数值模拟和模型试验等方面对箱形梁桥力学分析提出过许多新方法、新理论[1, 2]。但既有研究主要集中在静载范围的竖向集中和均布荷载,对于温度荷载作用下箱形梁桥力学性能及剪力滞后效应的研究尚不丰富[3- 5]。因而,现针对温度效应影响,箱形梁桥悬臂施工的力学特性展开精细化分析。其研究成果将为混凝土箱形梁桥温度应力的计算提供参考,同时也为桥梁施工监控提供理论和技术支持[5, 6]。
事实上20 世纪中期,德国学者就已开始研究温度应力对混凝土结构裂缝产生的影响。但是,近年来国内外研究大多集中于成桥后温度荷载对桥梁力学性能的作用,然而在桥梁施工过程中温度变化对桥梁的影响较为突出,且不容忽视。因为施工过程中箱形梁桥的力学状态极大地影响了成桥后桥梁结构的耐久性[7, 8]。研究温度效应对桥梁结构的作用,对于分析施工监控中箱形梁桥所受温度影响具有指导和借鉴意义,进而使成桥后的桥梁线形和结构受力满足设计要求[8- 10]。因而,该项研究对于改善结构力学性能、保证结构安全具有一定理论和工程实用价值。
1 温度效应理论及温度应力产生原因
1.1 温度场分布
混凝土箱梁由于内部水化热和外界太阳辐射,以及气温等变化的影响,结构内部处于不同的温度状态,每时每刻都将发生变化,因而影响混凝土箱梁温度分布的因素可分为内因和外因两部分。(1)外界因素对温度分布的影响:自然环境中的混凝土箱梁,受大气温度变化的作用,如夜间降温、太阳辐射、寒流、风雨等各种气象因素作用。这些因素一年四季、每天甚至每时每刻都在发生变化。一般在每年的七月至八月出现最高气温,且在每天的12 时至15 时出现最大值,而最低气温一般在每年的一月至二月的夜间出现。(2)内部条件影响:混凝土箱形梁桥温度分布的内部因素,主要由混凝土的热物理性、构件的形状、铺装层的厚度和颜色等决定。混凝土导热系数小,内部温度变化存在明显的滞后现象,导致混凝土内部所得到或扩散的热量有较大的差异,进而形成非线性分布的温度状态。
1.2 温度应力产生原因
温度应力按产生的原因通常分为常年温差应力和局部温差应力。常年温差应力是指在长时间的外部环境变化作用下箱形梁桥整体产生的温度应力,若结构无水平约束,将不会产生水平温度应力。在日照作用下,桥梁结构会出现局部温差而产生温度应力。当箱梁桥在日照作用下,因桥梁所处地理位置、风向、日照时间等诸多不确定随机因素的存在,使得箱梁截面内部和外部因温差对流、日照辐射、热传导不均而产生不均匀的温度分布,这便形成了温度场。温度场可由温度梯度来表示,温度梯度又分为线性变化的温度梯度和非线性变化的温度梯度,进而产生较大的温度应力。
2 温度效应的有限元分析
由于温度分布及桥梁结构的复杂性,要求得到混凝土箱形梁桥温度应力的精确解十分困难。因而,在实际工程中,通常基于力学知识做出假设,对模型进行相应简化。另一方面,如果采用不适当的简化计算模型,则会使计算结果产生较大误差。事实上,在温度荷载作用下,箱形梁发生弯曲变形会产生剪力滞后效应,只要箱梁的腹板间距较大,截面的变形就不满足平截面假定,即梁结构弯曲的初等梁理论。此时,要基于热弹性理论对混凝土箱梁的温度应力进行准确分析,则必须利用空间有限元和有限差分法等数值计算方法完成。
空间有限元法为将空间结构离散为有限个数目的单元,进而构造出空间单元的位移函数,然后利用位移—应变方程、应力—应变方程,得到箱形梁空间单元的刚度矩阵,再将单元刚度矩阵组集起来,形成整体刚度矩阵。进而,因温度改变而引起的单元节点等效荷载可以表示为:
![]()
式中:[B]T 为相关形函数的矩阵;[D]为弹性矩阵;T 为单元内任一点温度;α 为结构线膨胀系数。
在求出等效节点荷载后按通常求解应力方法解得由于温度效应而引起的节点位移δ,然后由δ根据方程式[σ]=[D][ε]=[D][B][δ]e 求得混凝土箱梁的温度应力。
3 国内设计规范中温度荷载的规定
不同混凝土结构的温度分布各有特点,各不相同,即使是在同一混凝土结构中,如钢筋混凝土箱梁中,它的温度分布也变化多样。因而,对于这样复杂的温度分布,研究中不可能分析计算每一瞬间的温度分布。从工程分析来讲,只需从各种复杂的温度分布中,选取某几种特定的温度分布,也即对混凝土箱梁的温差应力产生最不利影响的几种温度分布。据此,可以确定对箱形结构受力影响最大的所谓控制温度荷载,这就需要更为简捷、适用的计算方法。国内外桥梁工作者对此作了大量的研究工作,制定了适于本国混凝土桥梁结构温度梯度模式的规范(见图1)。
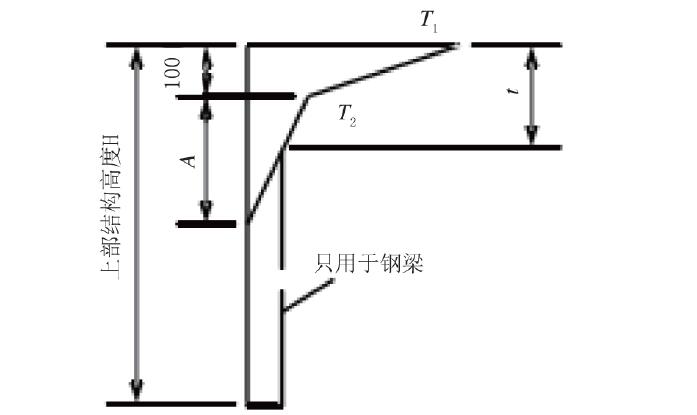
图1 中国公路桥规梯度温度示意图(单位:mm)
4 混凝土箱梁有限元模型的建立
根据实际情况,现简化并建立钢筋混凝土悬臂箱梁模型,以此分析研究悬臂箱梁在自重及日照温差作用下,其固定端应力及剪力滞效应的变化规律。箱梁模型为单箱单室矩形截面,跨径L 为30 m,且其截面尺寸如图2 所示。

图2 悬臂箱梁横截面图(单位:m)
箱梁结构材料选用C50 混凝土。材料参数:弹性模量E=3.5×104 MPa;G=1.4×104 MPa,泊松比μ=0.2,密度γ=25 kN/m3,线膨胀系数α=1.0×10- 5。日照温差荷载选用《公路桥梁设计规范》(JTGD60- 2004)中规定的温度梯度模式,桥梁上部结构类型为混凝土铺装。日照正温差(升温情况)基数T1=25℃,T2=6.7℃,日照反温差(降温情况) 基数T1=- 12.5℃,T2=- 3.35℃。有限元模型采用混凝土实体单元SOLID65,由于模型几何尺寸对称,故可用映射网格划分。上下翼缘横向划分尺寸为0.255 m,竖向划分为0.0625 m,腹板横向划分尺寸为0.2 m,竖向划分为0.075 m,桥梁沿纵向划分尺寸为0.5 m。对于支座约束模拟,悬臂固支端截面所有节点均设定为刚性约束,有限元实体模型如图3 所示。图4 为箱形梁桥悬壁施工效果图。

图3 悬臂箱梁有限元实体模型

图4 箱形梁桥悬臂施工效果图
5 有限元数值模拟分析
5.1 固端截面正应力分布
图5 为悬臂箱梁固支端截面应力分布图。
5.2 固端截面剪力滞效应分析
图6 为悬壁箱梁固支端截面剪滞系数分布图。
图5、图6 表明:
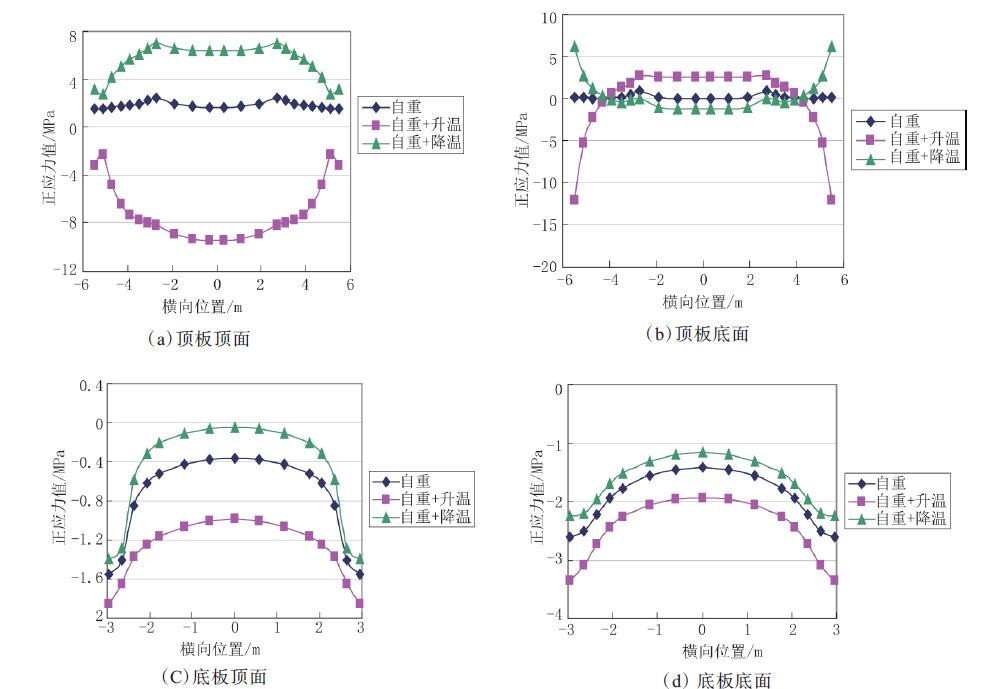
图5 悬臂箱梁固支端截面应力分布图

图6 悬臂箱梁固支端截面剪滞系数分布图
(1)在悬臂施工中,箱梁固支端截面在日照温差和自重作用下,皆表现为明显的剪力滞现象,但顶板顶面的应力集中现象更加严重。尽管顶板顶面和顶板底面的受力特点大致相反,但顶板底面的剪力滞后效应更为突出。
(2)同样,在自重和日照温差作用下,悬臂箱梁固支端底板顶面和底板底面亦皆受剪力滞后效应影响,但底板底面的应力更为突出,底板顶面的剪力滞后效应更加显著。
(3)悬臂施工,按桥梁规范温度荷载计算,箱梁自重产生的应力较小,而温度荷载产生的应力更大。
(4)悬臂箱梁固支端截面在日照温差作用下,其剪力滞后效应较自重单独作用更加复杂,且尽管箱梁顶板顶面的剪滞系数较小,但其应力集中现象最为突出。该现象应该引起施工监控和设计者的关注。
6 结论
(1)本文应用有限元数值模拟,分析了箱梁悬臂施工状态,温度效应对箱梁悬臂端力学性能的影响。其方法有益于桥梁施工监控的准确把握。
(2)箱形梁桥施工监控受温度、自重、收缩徐变等诸多因素的影响。而温度参数是一个受环境、材料、气候影响的随机变量,同时又是最难识别的参数之一。但它对箱梁施工监控中应力和挠度的影响较大。所以在桥梁监控中,应引起足够的重视。
(3)研究显示:在温度荷载影响下,箱梁翼板表现为明显的剪力滞现象,即:翼板和腹板相交处应力集中较为突出。
本文所用的研究方法,对箱形梁施工监控、耐久性设计具有一定指导意义。因而,本文的研究成果具有良好的理论意义和工程实用价值。
摘自:城市道桥与防洪






